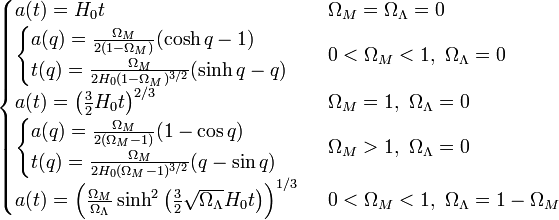Checked content

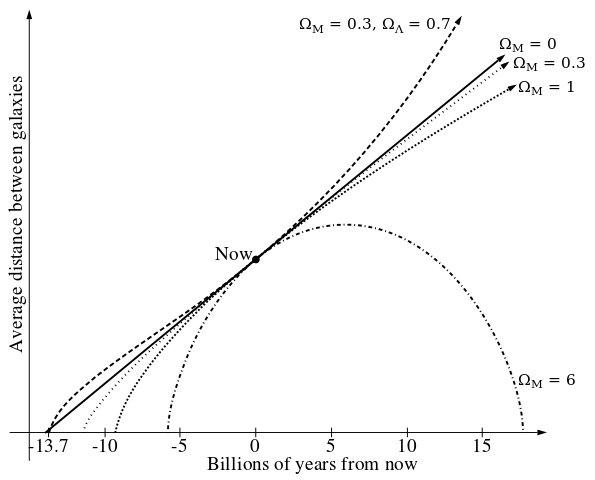
File:Friedmann universes.svg

Contents

Summary

Description

Intended as a replacement for File:Universe.svg and File:Universos.gif. Improvements: better dash patterns, more accurate curves (actual solutions of the Friedmann equations, not hand-drawn).
Date 23 September 2009
Source Own work
Author BenRG
Permission
( Reusing this file)

Public domain

Formulas

This diagram uses the following exact solutions to the Friedmann equations:

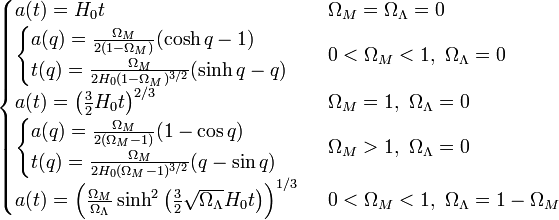
\begin{cases} a(t) = H_0 t & \Omega_M = \Omega_\Lambda = 0 \\ \begin{cases} a(q) = \tfrac{\Omega_M}{2(1-\Omega_M)} (\cosh q - 1) \\ t(q) = \tfrac{\Omega_M}{2H_0(1-\Omega_M)^{3/2}} (\sinh q - q) \end{cases} & 0 < \Omega_M < 1,\ \Omega_\Lambda = 0 \\ a(t) = \left( \tfrac32 H_0 t \right)^{2/3} & \Omega_M = 1,\ \Omega_\Lambda = 0 \\ \begin{cases} a(q) = \tfrac{\Omega_M}{2(\Omega_M-1)} (1-\cos q) \\ t(q) = \tfrac{\Omega_M}{2H_0(\Omega_M-1)^{3/2}} (q - \sin q) \end{cases} & \Omega_M > 1,\ \Omega_\Lambda = 0 \\ a(t) = \left( \tfrac{\Omega_M}{\Omega_\Lambda} \sinh^2 \left( \tfrac32 \sqrt{\Omega_\Lambda} H_0 t \right) \right)^{1/3} & 0 < \Omega_M < 1,\ \Omega_\Lambda = 1 - \Omega_M \end{cases}

See also

Some of the shown models are implemented as an animation at Cosmos-animation.

Licensing

Public domain I, the copyright holder of this work, release this work into the public domain. This applies worldwide.
In some countries this may not be legally possible; if so:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.

Tango-style info icon.svg The categories of this image should be checked. Check them now!

  • Remove redundant categories and try to put this image in the most specific category/categories
  • Remove this template by clicking here (or on the first line)

File usage on other wikis

Related galleries

The following pages on Schools Wikipedia link to this image (list may be incomplete):

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it. If the file has been modified from its original state, some details may not fully reflect the modified file.

Learn more

This selection has made Wikipedia available to all children. SOS Children is a global charity founded in 1949 to give children who have lost everything the childhood they deserve. Help another child by taking out a sponsorship.