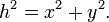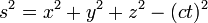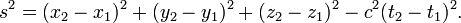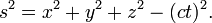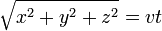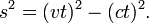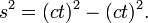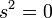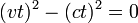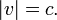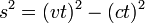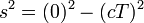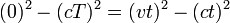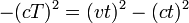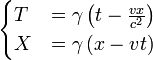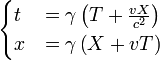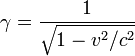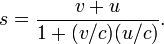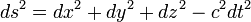Introduction to special relativity

In physics, special relativity is a fundamental theory concerning space and time, developed by Albert Einstein in 1905 as a modification of Galilean relativity. (See " History of special relativity" for a detailed account and the contributions of Hendrik Lorentz and Henri Poincaré.) The theory was able to explain some pressing theoretical and experimental issues in the physics of the time involving light and electrodynamics, such as the failure of the 1887 Michelson–Morley experiment, which aimed to measure differences in the relative speed of light due to the Earth's motion through the hypothetical, and now discredited, luminiferous aether. The aether was then considered to be the medium of propagation of electromagnetic waves such as light.

Einstein postulated that the speed of light in free space is the same for all observers, regardless of their motion relative to the light source, where we may think of an observer as an imaginary entity with a sophisticated set of measurement devices, at rest with respect to itself, that perfectly record the positions and times of all events in space and time. This postulate stemmed from the assumption that Maxwell's equations of electromagnetism, which predict a specific speed of light in a vacuum, hold in any inertial frame of reference rather than, as was previously believed, just in the frame of the aether. This prediction contradicted the laws of classical mechanics, which had been accepted for centuries, by arguing that time and space are not fixed and in fact change to maintain a constant speed of light regardless of the relative motions of sources and observers. Einstein's approach was based on thought experiments, calculations, and the principle of relativity, which is the notion that all physical laws should appear the same (that is, take the same basic form) to all inertial observers. Today, scientists are so comfortable with the idea that the speed of light is always the same that the metre is now defined as "the length of the path travelled by light in vacuum during a time interval of 1/299 792 458 of a second." This means that the speed of light is by convention 299 792 458 m/s (approximately 1.079 billion kilometres per hour, or 671 million miles per hour).

The predictions of special relativity are almost identical to those of Galilean relativity for most everyday phenomena, in which speeds are much lower than the speed of light, but it makes different, non-obvious predictions for objects moving at very high speeds. These predictions have been experimentally tested on numerous occasions since the theory's inception and were confirmed by those experiments. The major predictions of special relativity are:

• Relativity of simultaneity: Observers who are in motion with respect to each other may disagree on whether two events occurred at the same time or one occurred before the other.
• Time dilation (An observer watching two identical clocks, one moving and one at rest, will measure the moving clock to tick more slowly)
• Length contraction (Along the direction of motion, a rod moving with respect to an observer will be measured to be shorter than an identical rod at rest), and
• The equivalence of mass and energy (written as E = mc²).

Special relativity predicts a non-linear velocity addition formula which prevents speeds greater than that of light from being observed. In 1908, Hermann Minkowski reformulated the theory based on different postulates of a more geometrical nature. This approach considers space and time as being different components of a single entity, the spacetime, which is "divided" in different ways by observers in relative motion. Likewise, energy and momentum are the components of the four-momentum, and the electric and magnetic field are the components of the electromagnetic tensor.

As Galilean relativity is now considered an approximation of special relativity valid for low speeds, special relativity is considered an approximation of the theory of general relativity valid for weak gravitational fields. General relativity postulates that physical laws should appear the same to all observers (an accelerating frame of reference being equivalent to one in which a gravitational field acts), and that gravitation is the effect of the curvature of spacetime caused by energy (including mass).

Classical physics and electromagnetism

Through the era between Newton and around the start of the 20th century, the development of classical physics had made great strides. Newton's application of the inverse square law to gravity was the key to unlocking a wide variety of physical events, from heat to light, and calculus made the direct calculation of these effects tractable. Over time, new mathematical techniques, notably the Lagrangian, greatly simplified the application of these physical laws to more complex problems.

As electricity and magnetism were better explored, it became clear that the two concepts were related. Over time, this work culminated in Maxwell's equations, a set of four equations that could be used to calculate the entirety of electromagnetism. One of the most interesting results of the application of these equations was that it was possible to construct a self-sustaining wave of electrical and magnetic fields that could propagate through space. When reduced, the math demonstrated that the speed of propagation was dependent on two universal constants, and their ratio was the speed of light. Light was an electromagnetic wave.

Under the classic model, waves are displacements within a medium. In the case of light, the waves were thought to be displacements of a special medium known as the luminiferous aether, which extended through all space. This being the case, light travels in its own frame of reference, the frame of the aether. According to the Galilean transform, we should be able to measure the difference in velocities between the aether's frame and any other – a universal frame at last.

Designing an experiment to actually carry out this measurement proved very difficult, however, as the speeds and timing involved made accurate measurement difficult. The measurement problem was eventually solved with the Michelson–Morley experiment. To everyone's surprise, no relative motion was seen. Either the aether was travelling at the same velocity as the Earth, difficult to imagine given the Earth's complex motion, or there was no aether. Follow-up experiments tested various possibilities, and by the start of the 20th century it was becoming increasingly difficult to escape the conclusion that the aether did not exist.

These experiments all showed that light simply did not follow the Galilean transformation. And yet it was clear that physical objects emitted light, which led to unsolved problems. If one were to carry out the experiment on the train by "throwing light" instead of balls, if light does not follow the Galilean transformation then the observers should not agree on the results. Yet it was apparent that the universe disagreed; physical systems known to be at great speeds, like distant stars, had physics that were as similar to our own as measurements allowed. Some sort of transformation had to be acting on light, or better, a single transformation for both light and matter.

The development of a suitable transformation to replace the Galilean transformation is the basis of special relativity.

Invariance of length: the Euclidean picture

In special relativity, space and time are joined into a unified four-dimensional continuum called spacetime. To gain a sense of what spacetime is like, we must first look at the Euclidean space of classical Newtonian physics. This approach to explaining the theory of special relativity begins with the concept of " length".

In everyday experience, it seems that the length of objects remains the same no matter how they are rotated or moved from place to place; as a result the simple length of an object doesn't appear to change or is invariant. However, as is shown in the illustrations below, what is actually being suggested is that length seems to be invariant in a three-dimensional coordinate system.

The length of a line in a two-dimensional Cartesian coordinate system is given by Pythagoras' theorem:

One of the basic theorems of vector algebra is that the length of a vector does not change when it is rotated. However, a closer inspection tells us that this is only true if we consider rotations confined to the plane. If we introduce rotation in the third dimension, then we can tilt the line out of the plane. In this case the projection of the line on the plane will get shorter. Does this mean the line's length changes? – obviously not. The world is three-dimensional and in a 3D Cartesian coordinate system the length is given by the three-dimensional version of Pythagoras's theorem:

This is invariant under all rotations. The apparent violation of invariance of length only happened because we were "missing" a dimension. It seems that, provided all the directions in which an object can be tilted or arranged are represented within a coordinate system, the length of an object does not change under rotations. With time and space considered to be outside the realm of physics itself, under classical mechanics a 3-dimensional coordinate system is enough to describe the world.

Note that invariance of length is not ordinarily considered a principle or law, not even a theorem. It is simply a statement about the fundamental nature of space itself. Space as we ordinarily conceive it is called a three-dimensional Euclidean space, because its geometrical structure is described by the principles of Euclidean geometry. The formula for distance between two points is a fundamental property of a Euclidean space, it is called the Euclidean metric tensor (or simply the Euclidean metric). In general, distance formulas are called metric tensors.

Note that rotations are fundamentally related to the concept of length. In fact, one may define length or distance to be that which stays the same (is invariant) under rotations, or define rotations to be that which keep the length invariant. Given any one, it is possible to find the other. If we know the distance formula, we can find out the formula for transforming coordinates in a rotation. If, on the other hand, we have the formula for rotations then we can find out the distance formula.

The Minkowski formulation: introduction of spacetime

After Einstein derived special relativity formally from the (at first sight counter-intuitive) assumption that the speed of light is the same to all observers, Hermann Minkowski built on mathematical approaches used in non-euclidean geometry and on the mathematical work of Lorentz and Poincaré. Minkowski showed in 1908 that Einstein's new theory could also be explained by replacing the concept of a separate space and time with a four-dimensional continuum called spacetime. This was a groundbreaking concept, and Roger Penrose has said that relativity was not truly complete until Minkowski reformulated Einstein's work.

The concept of a four-dimensional space is hard to visualise. It may help at the beginning to think simply in terms of coordinates. In three-dimensional space, one needs three real numbers to refer to a point. In the Minkowski space, one needs four real numbers (three space coordinates and one time coordinate) to refer to a point at a particular instant of time. This point, specified by the four coordinates, is called an event. The distance between two different events is called the spacetime interval.

A path through the four-dimensional spacetime (usually known as Minkowski space) is called a world line. Since it specifies both position and time, a particle having a known world line has a completely determined trajectory and velocity. This is just like graphing the displacement of a particle moving in a straight line against the time elapsed. The curve contains the complete motional information of the particle.

In the same way as the measurement of distance in 3D space needed all three coordinates, we must include time as well as the three space coordinates when calculating the distance in Minkowski space (henceforth called M). In a sense, the spacetime interval provides a combined estimate of how far apart two events occur in space as well as the time that elapses between their occurrence.

But there is a problem; time is related to the space coordinates, but they are not equivalent. Pythagoras' theorem treats all coordinates on an equal footing (see Euclidean space for more details). We can exchange two space coordinates without changing the length, but we can not simply exchange a space coordinate with time – they are fundamentally different. It is an entirely different thing for two events to be separated in space and to be separated in time. Minkowski proposed that the formula for distance needed a change. He found that the correct formula was actually quite simple, differing only by a sign from Pythagoras' theorem:

where c is a constant and t is the time coordinate. Multiplication by c, which has the dimensions L T ⁻¹, converts the time to units of length and this constant has the same value as the speed of light. So the spacetime interval between two distinct events is given by

There are two major points to be noted. Firstly, time is being measured in the same units as length by multiplying it by a constant conversion factor. Secondly, and more importantly, the time-coordinate has a different sign than the space coordinates. This means that in the four-dimensional spacetime, one coordinate is different from the others and influences the distance differently. This new "distance" may be zero or even negative. This new distance formula, called the metric of the spacetime, is at the heart of relativity. This distance formula is called the metric tensor of M. This minus sign means that a lot of our intuition about distances can not be directly carried over into spacetime intervals. For example, the spacetime interval between two events separated both in time and space may be zero (see below). From now on, the terms distance formula and metric tensor will be used interchangeably, as will be the terms Minkowski metric and spacetime interval.

In Minkowski spacetime the spacetime interval is the invariant length, the ordinary 3D length is not required to be invariant. The spacetime interval must stay the same under rotations, but ordinary lengths can change. Just like before, we were missing a dimension. Note that everything thus far is merely definitions. We define a four-dimensional mathematical construct which has a special formula for distance, where distance means that which stays the same under rotations (alternatively, one may define a rotation to be that which keeps the distance unchanged).

Now comes the physical part. Rotations in Minkowski space have a different interpretation than ordinary rotations. These rotations correspond to transformations of reference frames. Passing from one reference frame to another corresponds to rotating the Minkowski space. An intuitive justification for this is given below, but mathematically this is a dynamical postulate just like assuming that physical laws must stay the same under Galilean transformations (which seems so intuitive that we don't usually recognise it to be a postulate).

Since by definition rotations must keep the distance same, passing to a different reference frame must keep the spacetime interval between two events unchanged. This requirement can be used to derive an explicit mathematical form for the transformation that must be applied to the laws of physics (compare with the application of Galilean transformations to classical laws) when shifting reference frames. These transformations are called the Lorentz transformations. Just like the Galilean transformations are the mathematical statement of the principle of Galilean relativity in classical mechanics, the Lorentz transformations are the mathematical form of Einstein's principle of relativity. Laws of physics must stay the same under Lorentz transformations. Maxwell's equations and Dirac's equation satisfy this property, and hence they are relativistically correct laws (but classically incorrect, since they don't transform correctly under Galilean transformations).

With the statement of the Minkowski metric, the common name for the distance formula given above, the theoretical foundation of special relativity is complete. The entire basis for special relativity can be summed up by the geometric statement "changes of reference frame correspond to rotations in the 4D Minkowski spacetime, which is defined to have the distance formula given above". The unique dynamical predictions of SR stem from this geometrical property of spacetime. Special relativity may be said to be the physics of Minkowski spacetime. In this case of spacetime, there are six independent rotations to be considered. Three of them are the standard rotations on a plane in two directions of space. The other three are rotations in a plane of both space and time: These rotations correspond to a change of velocity, and the Minkowski diagrams devised by him describe such rotations.

As has been mentioned before, one can replace distance formulas with rotation formulas. Instead of starting with the invariance of the Minkowski metric as the fundamental property of spacetime, one may state (as was done in classical physics with Galilean relativity) the mathematical form of the Lorentz transformations and require that physical laws be invariant under these transformations. This makes no reference to the geometry of spacetime, but will produce the same result. This was in fact the traditional approach to SR, used originally by Einstein himself. However, this approach is often considered to offer less insight and be more cumbersome than the more natural Minkowski formalism.

Einstein's postulate: the constancy of the speed of light

Einstein's postulate that the speed of light is a constant comes out as a natural consequence of the Minkowski formulation.

Proposition 1:

When an object is travelling at c in a certain reference frame, the spacetime interval is zero.

Proof:

The spacetime interval between the origin-event (0,0,0,0) and an event (x,y,z,t) is

The distance travelled by an object moving at velocity v for t seconds is:

giving

Since the velocity v equals c we have

Hence the spacetime interval between the events of departure and arrival is given by

Proposition 2:

An object travelling at c in one reference frame is travelling at c in all reference frames.

Proof:

Let the object move with velocity v when observed from a different reference frame. A change in reference frame corresponds to a rotation in M. Since the spacetime interval must be conserved under rotation, the spacetime interval must be the same in all reference frames. In proposition 1 we showed it to be zero in one reference frame, hence it must be zero in all other reference frames. We get that

which implies

The paths of light rays have a zero spacetime interval, and hence all observers will obtain the same value for the speed of light. Therefore, when assuming that the universe has four dimensions that are related by Minkowski's formula, the speed of light appears as a constant, and does not need to be assumed (postulated) to be constant as in Einstein's original approach to special relativity.

Clock delays and rod contractions: more on Lorentz transformations

Another consequence of the invariance of the spacetime interval is that clocks will appear to go slower on objects that are moving relative to the observer. This is very similar to how the 2D projection of a line rotated into the third-dimension appears to get shorter. Length is not conserved simply because we are ignoring one of the dimensions. Let us return to the example of John and Bill.

John observes the length of Bill's spacetime interval as:

whereas Bill doesn't think he has traveled in space, so writes:

The spacetime interval, s², is invariant. It has the same value for all observers, no matter who measures it or how they are moving in a straight line. This means that Bill's spacetime interval equals John's observation of Bill's spacetime interval so:

and

hence

.

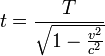So, if John sees a clock that is at rest in Bill's frame record one second, John will find that his own clock measures between these same ticks an interval t, called coordinate time, which is greater than one second. It is said that clocks in motion slow down, relative to those on observers at rest. This is known as "relativistic time dilation of a moving clock". The time that is measured in the rest frame of the clock (in Bill's frame) is called the proper time of the clock.

In special relativity, therefore, changes in reference frame affect time also. Time is no longer absolute. There is no universally correct clock; time runs at different rates for different observers.

Similarly it can be shown that John will also observe measuring rods at rest on Bill's planet to be shorter in the direction of motion than his own measuring rods. This is a prediction known as "relativistic length contraction of a moving rod". If the length of a rod at rest on Bill's planet is X, then we call this quantity the proper length of the rod. The length x of that same rod as measured on John's planet, is called coordinate length, and given by

.

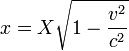These two equations can be combined to obtain the general form of the Lorentz transformation in one spatial dimension:

or equivalently:

where the Lorentz factor is given by

The above formulas for clock delays and length contractions are special cases of the general transformation.

Alternatively, these equations for time dilation and length contraction (here obtained from the invariance of the spacetime interval), can be obtained directly from the Lorentz transformation by setting X = 0 for time dilation, meaning that the clock is at rest in Bill's frame, or by setting t = 0 for length contraction, meaning that John must measure the distances to the end points of the moving rod at the same time.

A consequence of the Lorentz transformations is the modified velocity-addition formula:

Simultaneity and clock desynchronisation

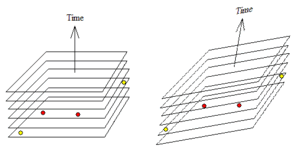
The last consequence of Minkowski's spacetime is that clocks will appear to be out of phase with each other along the length of a moving object. This means that if one observer sets up a line of clocks that are all synchronised so they all read the same time, then another observer who is moving along the line at high speed will see the clocks all reading different times. This means that observers who are moving relative to each other see different events as simultaneous. This effect is known as "Relativistic Phase" or the "Relativity of Simultaneity". Relativistic phase is often overlooked by students of special relativity, but if it is understood, then phenomena such as the twin paradox are easier to understand.

Observers have a set of simultaneous events around them that they regard as composing the present instant. The relativity of simultaneity results in observers who are moving relative to each other having different sets of events in their present instant.

The net effect of the four-dimensional universe is that observers who are in motion relative to you seem to have time coordinates that lean over in the direction of motion, and consider things to be simultaneous that are not simultaneous for you. Spatial lengths in the direction of travel are shortened, because they tip upwards and downwards, relative to the time axis in the direction of travel, akin to a skew or shear of three-dimensional space.

Great care is needed when interpreting spacetime diagrams. Diagrams present data in two dimensions, and cannot show faithfully how, for instance, a zero length spacetime interval appears.

General relativity: a peek forward

Unlike Newton's laws of motion, relativity is not based upon dynamical postulates. It does not assume anything about motion or forces. Rather, it deals with the fundamental nature of spacetime. It is concerned with describing the geometry of the backdrop on which all dynamical phenomena take place. In a sense therefore, it is a meta-theory, a theory that lays out a structure that all other theories must follow. In truth, special relativity is only a special case. It assumes that spacetime is flat. That is, it assumes that the structure of Minkowski space and the Minkowski metric tensor is constant throughout. In general relativity, Einstein showed that this is not true. The structure of spacetime is modified by the presence of matter. Specifically, the distance formula given above is no longer generally valid except in space free from mass. However, just like a curved surface can be considered flat in the infinitesimal limit of calculus, a curved spacetime can be considered flat at a small scale. This means that the Minkowski metric written in the differential form is generally valid.

One says that the Minkowski metric is valid locally, but it fails to give a measure of distance over extended distances. It is not valid globally. In fact, in general relativity the global metric itself becomes dependent on the mass distribution and varies through space. The central problem of general relativity is to solve the famous Einstein field equations for a given mass distribution and find the distance formula that applies in that particular case. Minkowski's spacetime formulation was the conceptual stepping stone to general relativity. His fundamentally new outlook allowed not only the development of general relativity, but also to some extent quantum field theories.

Mass–energy equivalence: sunlight and atom bombs

Einstein showed that mass is simply another form of energy. The energy equivalent of rest mass m is mc². This equivalence implies that mass should be interconvertible with other forms of energy. This is the basic principle behind atom bombs and production of energy in nuclear reactors and stars (like the Sun).

Applications

There is a common perception that relativistic physics is not needed for practical purposes or in everyday life. This is not true. Without relativistic effects, gold would look silvery, rather than yellow. Many technologies are critically dependent on relativistic physics:

• Cathode ray tubes,
• Particle accelerators,
• Global Positioning System (GPS) – although this really requires the full theory of general relativity

The postulates of special relativity

Einstein developed special relativity on the basis of two postulates:

• First postulate – Special principle of relativity – The laws of physics are the same in all inertial frames of reference. In other words, there are no privileged inertial frames of reference.
• Second postulate – Invariance of c – The speed of light in a vacuum is independent of the motion of the light source.

Special relativity can be derived from these postulates, as was done by Einstein in 1905. Einstein's postulates are still applicable in the modern theory but the origin of the postulates is more explicit. It was shown above how the existence of a universally constant velocity (the speed of light) is a consequence of modeling the universe as a particular four-dimensional space having certain specific properties. The principle of relativity is a result of Minkowski structure being preserved under Lorentz transformations, which are postulated to be the physical transformations of inertial reference frames.